티스토리 뷰
JVM 기반의 언어를 사용할 때 보통 돈 같은 필드는 타입을 BigDecimal로 사용하는 경우가 많습니다. 그리고 필자도 개인 프로젝트를 하면서 돈과 관련된 필드는 무조건 BigDecimal을 사용했습니다.
그 이유가 궁금해서 찾아보면서 깊게 알아본 내용들을 바탕으로 정리해보겠습니다.
부동 소수점이란?
BigDecimal을 쓰게된 이유를 찾기 위해선 부동 소수점이라는 개념을 먼저 알고 있어야합니다. 보통 PC에서 실수를 표현하고 연산할 때 소수점의 위치가 고정되어있는 것이 아닌 움직일 수 있는 경우를 부동 소수점이라고 합니다.
IEEE 754 표준으로 보면 다음과 같이 표현할 수 있습니다.
단정 밀도의 경우
- 부호 : 1비트
- 지수 : 8비트
- 가수 : 23비트
배정 밀도의 경우
- 부호 : 1비트
- 지수 : 11비트
- 가수 : 52비트
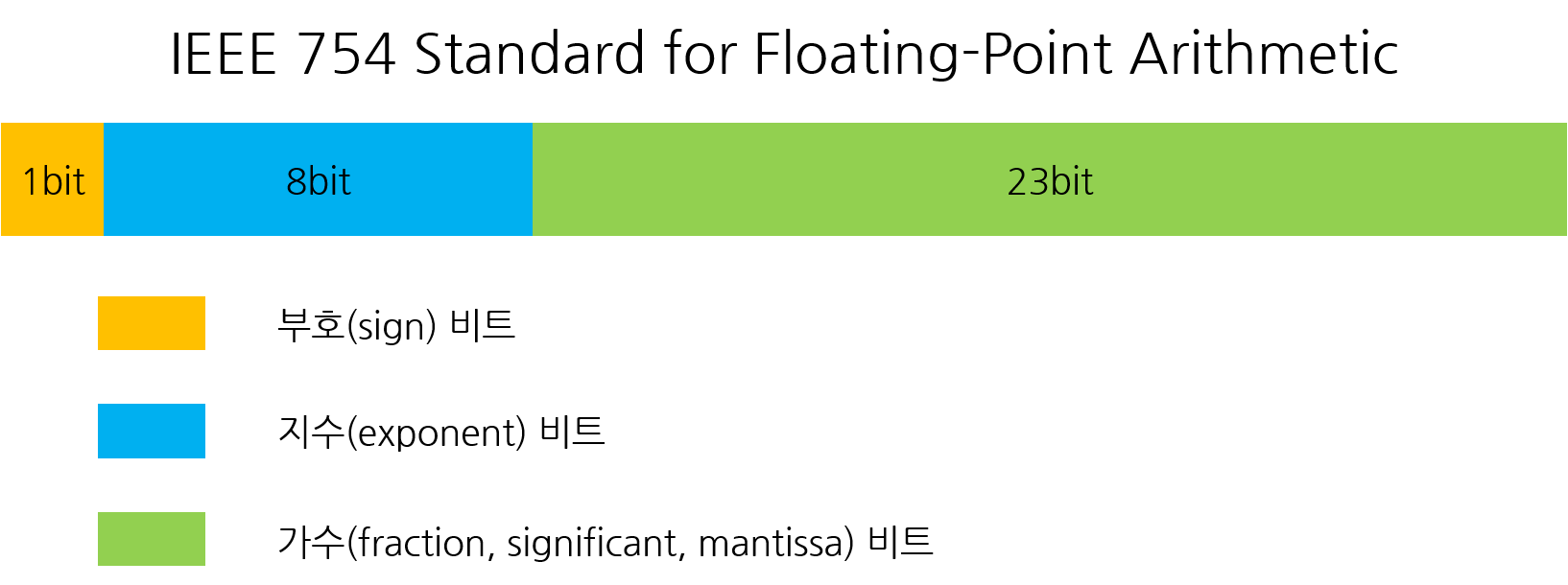
여기서 부호는 음수/양수를 표현, 가수는 실제 숫자 값을 표현 그리고 지수는 소수점의 위치를 결정합니다.
부동 소수점의 한계?
부동소수점에 대해서 알아보았습니다. 근데 여기서 문제점을 발견하신 분도 계실겁니다. 배정 밀도로 표현한다 한들 최대 52비트까지만 숫자를 표현할 수 없다는 겁니다.
대표적인 예로 0.1(10진수)를 2진수로 표현해볼가요?

계속해서 무한이 반복되는 하나의 이진수가 생성됩니다. 그리고 부동 소수점은 이걸 52비트까지만 표현하겠죠. 그러면 숫자는 부정확한 값이 나타납니다.
fun main() {
var number: Double = 0.0
for (i in 1 .. 100) {
number += 0.1
}
println(number)
}다음 코드는 0.1을 100번 더하는 연산입니다. 연산을 하면 당연히 100번 0.1을 더했으므로 10이 나와야합니다. 하지만 결과 값은 다음과 같습니다.

뭔가 예상한 값이랑 많이 다르게 나옵니다.
이것이 바로 부동 소수점의 한계를 나타내는 대표적인 예입니다. 이진 표현법으로 소수점을 제대로 표현할 수 없기 때문에 double형인 number 자료형은 52비트까지만 표현을 했고 그 과정에서 값이 변질되어 올바른 값대로 연산되지 않았습니다.
실제로 그럼 어떻게 표현되고 있을까요?
fun main() {
val number = 0.1
val bits = java.lang.Double.doubleToLongBits(number)
val binaryRepresentation = bits.toString(2).padStart(64, '0')
println("binary representation: $binaryRepresentation")
}binary representation: 0011111110111001100110011001100110011001100110011001100110011010
무한히 반복되는 수여야 하지만 그렇지 않고 일부만 표현되고 있습니다.
이게 은행 시스템이었다면 소비자들은 부동 소수점으로인해 본인이 원하는 금액보다 낮거나 높은 금액을 반환받을 것이며 이는 쌓이면 현금을 관리하는 입장에선 매우 치명적일 수 있습니다.
그럼 어떻게 해결해야할까?
여기서 BigDecimal을 쓰는 이유가 나옵니다. 문제를 되살펴보면 다음과 같습니다.
1. 부동 소수점은 이진 표현법으로 무한히 이어질 때 특정 비트까지만 표현하여 올바른 값을 표현 못한다.
2. 이로인해 연산이 부정확하게 일어난다.
이를 해결하기 위한 가장 빠른 방법은 십진수로 연산하는 방법입니다. 하지만 컴퓨터는 이진 표현법 밖에 모릅니다. 그래서 JVM단에서는 BigDecimal을 지원합니다.
BigDecimal이란?
BigDecimal은 십진수를 표현하고 연산할 수 있는 라이브러리로 주요 목적은 부동 소수점에서 발생하는 근사값으로 인한 오차를 십진 연산을 수행함으로써 해결하는 것입니다.
BigDecimal은 다음과 같은 방법으로 문제를 풀어내고 있습니다.
- 정수 값과 정밀도를 나눠서 저장 (예를 들어 0.1의 경우 숫자를 정수로 표현하는 정수 값 1과 소수점 이하의 자릿수를 표현하는 정밀도 1로 나눠서 저장합니다.)
- 연산 정수 값에 연산을 수행하고 정밀도를 적용하여 최종 결과를 나타내어 정확한 계산을 유도합니다.
- 십진 표현을 사용하기 때문에 0.1을 정확하게 0.1로 표현할 수 있습니다.
- 불변성이 존재하기 때문에 Thread safe하게 정확한 연산을 수행합니다. 다만 이 경우 성능이 좀 떨어집니다.
사용 예시는 다음과 같습니다.
import java.math.BigDecimal
fun main() {
var number: BigDecimal = BigDecimal("0.0")
for (i in 1 .. 100) {
number = number.add(BigDecimal("0.1"))
}
println(number)
}
결과는 정확히 10이 나왔습니다.
위 원리를 이용하여 정확하게 소수점을 정확하게 계산해내고 부동 소수점처럼 문제가 발생하지 않습니다. 고로 우리는 금액같은 데이터도 안전하게 데이터를 관리할 수 있습니다.
마무리
부동 소수점에 대해 알아보며 컴퓨터에 부정확한 연산의 원인을 공부했고 그 해결책인 BigDecimal과 그 동작원리를 공부했습니다. 독자분들도 그냥 사용하고 넘기는 것이 아닌 자세히 알아보고 원리를 공부해보는건 어떨까요?
마침.
'CS' 카테고리의 다른 글
| Compiler 언어와 interpreter 언어는 정확하게 어떤 차이가 있을까? (2) | 2023.04.08 |
|---|
- Total
- Today
- Yesterday
- 개발자
- java
- 프로그래밍
- 취준
- 면접 준비
- 면접
- thread
- 백엔드
- 코드
- lock
- Redis
- IT
- 프로젝트
- 동시성
- JPA
- 인터뷰
- 개발
- 취업준비
- 코딩
- CS
- DB
- 취업
- MySQL
- docker
- 자바
- Spring
- DevOps
- Kotlin
- 면접준비
- 게시판
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
